1. LA GEOMETRÍA.
La geometría es una rama de la matemática que estudia idealizaciones del espacio: puntos, rectas, planos, polígonos, poliedros, curvas, superficies...
En el “mundo real” se utiliza para solucionar problemas concretos y es la justificación teórica de muchos instrumentos: compás, teodolito, pantógrafo... También da fundamento teórico a inventos como sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales). Es útil en la preparación de diseños (justificación teórica de la Geometría Descriptiva y del Dibujo Técnico), e incluso en la fabricación de artesanías.
1.1 Conceptos fundamentales.
La geometría se basa en tres conceptos fundamentales que se aceptan sin definirlos y que forman parte del espacio geométrico, o sea el conjunto formado por todos los puntos:
1.1.1 El punto.
Un punto se representa con una pequeña cruz y se lo designa con una letra de imprenta mayúscula.
1.1.2 La recta.
Una recta se representa con una porción de la misma y se la designa con una letra de imprenta minúscula.
1.1.3. El plano.
Un plano se representa con una porción del mismo y se lo designa con una letra griega.
1.2. Relaciones fundamentales.
Los tres conceptos anteriores están relacionados a través de las relaciones de pertenencia e inclusión:
- Los puntos pertenecen a las rectas y los planos.
- Las rectas están incluidas en los planos.
1.3 Postulados
Se llaman postulados a aquellas propiedades que satisfacen los elementos geométricos que se aceptan sin demostrar y que surgen de la simple observación.
1. Existen infinitos puntos, infinitas rectas e infinitos planos.
2. Todo punto pertenece a infinitas rectas, ya que por un punto pasan infinitas rectas.
El conjunto de rectas que concurren en un punto se denomina haz de rectas.
3. Toda recta está incluida en infinitos planos ya que por una recta pasan infinitos planos.
El conjunto de planos que pasa por una recta se denomina haz de planos.
4. Dos puntos determinan una y solo una recta a la cual pertenecen.
5. A una recta pertenecen infinitos puntos y existen también infinitos puntos que no pertenecen a ella.
6. Una recta y un punto fuera de ella determinan un plano de modo que el punto pertenece al mismo y la recta está incluida en el.
7. La recta determinada por dos puntos de un plano está incluida en dicho plano.
También puede enunciarse como: Dos puntos incluidos en un plano determinan una recta que está incluida en el plano.
8. A un plano pertenecen infinitos puntos y existen también infinitos puntos que no pertenecen a ella.
2. LA GEOMETRÍA PLANA.
La geometría plana es la rama de la geometría elemental que estudia las propiedades de superficies y figuras planas, como el triángulo o el circulo. Esta parte de la geometría también se conoce como geometría euclídea, en honor al matemático griego Euclides, el primero en estudiarla en el siglo IV a.C. Su extenso tratado Elementos de geometría se mantuvo como texto autorizado de geometría hasta la aparición de las llamadas geometrías no euclídeas en el siglo XIX.
2.1 Triángulo.
El triángulo es una figura plana limitada por tres segmentos (en este caso A, B y C).
Para nombrar un triángulo se puede usar las tres letras de sus vértices en cualquier orden, y sus lados por un par de estas letras (ej.: el triángulo: ABC, y los lados AB, BC y AC).
La base de un triángulo puede ser cualquiera de sus lados, pero una vez que se eligió un lado la altura es una sola: la menor distancia entre la base y el vértice opuesto.
- Clasificación de los triángulos según sus lados:
- Escaleno: No tiene lados iguales.
- Isósceles: Tiene dos lados iguales.
- Equilátero: Tiene los tres lados iguales.
- Clasificación de los triángulos según sus ángulos:
- Rectángulo: Tiene un Angulo recto.
- Obtusángulo: Tiene un Angulo obtuso.
- Acutángulo: Tiene sus tres ángulos agudos
- Propiedades y definiciones:
Propiedad 1: Los ángulos internos de un triángulo suman 180 grados.
Propiedad 2: En un triángulo rectángulo los ángulos que no son rectos son agudos.
Propiedad 3: En un triángulo solo puede haber, a lo sumo, un Angulo obtuso.
Propiedad 4: La suma de dos lados de un triángulo es mayor que el tercero.
2.2 Cuadrado.
El cuadrado es una figura plana limitada por cuatro segmentos, de forma tal que sus lados (AB=AC=CD=BD) y sus ángulos son todos iguales entre sí.
Los cuadrados tienen la particularidad de tener los ángulos iguales por lo que miden 90 grados cada uno.
Este hecho simplifica las fórmulas de perímetros y áreas.
Otra particularidad es que los cuadrados tienen dos diagonales iguales, y que el Ángulo formado por ellas es también de 90 grados.
- Propiedades y definiciones:
Acotación: Nótese que el cuadrado es un caso particular de rectángulo en donde su lado mayor es igual al lado menor, pero no todos los rectángulos cumplen con las propiedades de los cuadrados a continuación se dan algunas propiedades de cuadrados (si desea ver más seleccione las propiedades compartidas).
Propiedad 1: Las diagonales de un cuadrado forman ángulos iguales de 90 grados
Propiedad 2: Cada diagonal forma dos triángulos isósceles.
2.3. Rectángulo.
El rectángulo es una figura plana limitada por cuatro segmentos, de forma tal que tiene pares de lados iguales (AC=BD y AB=CD) y todos sus ángulos son iguales.
Los rectángulos tienen la particularidad de tener los ángulos iguales, por lo que miden 90 grados cada uno.
Este hecho simplifica las fórmulas de perímetros y áreas, aunque no tanto como en el cuadrado, ya que posee dos pares de lados iguales.
Acotación: Nótese que el cuadrado es un caso particular de rectángulo en donde su lado mayor es igual al lado menor, por lo que es de sorprender que todas las propiedades de los rectángulos se mantengan para los cuadrados, por lo que enunciaremos aquí las propiedades de los rectángulos, y estas se aplican a los cuadrados.
- Propiedades:
Propiedad 1: Los lados opuestos de un rectángulo son paralelos e iguales.
Propiedad 2: Las diagonales de un rectángulo se interceptan formando pares de ángulos opuestos iguales.
2.4. Circunferencia.
La circunferencia es una curva cerrada cuyos puntos están a igual distancia de otro fijo que se llama centro.
El radio es la distancia que hay entre el centro y algún punto de la circunferencia.
El radio de una circunferencia es la distancia que hay entre el centro y algún punto de la misma.
El diámetro de una circunferencia es la longitud de un segmento que une dos puntos de la circunferencia y pasa por el centro (es decir dos veces el radio).
- Propiedades y definiciones:
Secante de una circunferencia: Es cualquier recta que la corta en dos puntos.
Tangente a una circunferencia: Es cualquier recta que la toque en un punto y sólo en uno.
Arco: Es una parte de la circunferencia de un círculo.
Punto exterior a una circunferencia: Es cuando la distancia del punto al centro es mayor que el radio.
Punto interior de una circunferencia: Es cuando la distancia del punto al centro es menor que el radio.
Propiedad 1: Toda tangente a la circunferencia es perpendicular al radio.
Propiedad 2: Una recta es tangente a una circunferencia si es perpendicular al radio.
Propiedad 3: Dos circunferencias son iguales sí tienen el mismo centro y el mismo radio (o diámetro).
3. ÁREA DE FIGURAS PLANAS.
Vamos a estudiar ahora el área o superficie de las principales figuras planas que ya conocemos. Una vez establecidas las unidades que vamos a emplear para expresar el área calcularemos la superficie del rectángulo, que es muy sencilla. A partir del área del rectángulo se puede deducir la de cualquier otro paralelogramo, así como la del triángulo.
El conocimiento de la superficie del triángulo nos permitirá a su vez deducir la de un polígono regular cualquiera y, aumentando el número de lados del polígono, podremos calcular la superficie del círculo. Finalmente.calcularemos el área de ciertas partes del círculo. denominadas sector circular. segmento circular y corona circular.
3.1. Medidas de superficie.
La unidad fundamental de las medidas de superficie en el sistema métrico decimal es el metro cuadrado (m2). que se define como la superficie de un cuadrado de 1 metro de lado.
Los divisores del m2 son: dm2. cm2 y mm2. En la siguiente figura vemos un metro cuadrado cuyo lado se ha dividido en 10 partes. Con ello podemos verificar que en un metro cuadrado caben 100 dm2.
3.2. Área del rectángulo.
Supongamos que se ha dividido el lado mayor del rectángulo que llamaremos base, en 6 unidades de longitud; y el lado menor, que llamaremos altura, en 3 unidades de longitud. Entonces, podremos colocar en la superficie del rectángulo 3 filas de unidades cuadradas de forma que cada una de ellas cuente con 6 unidades cuadradas. En total:
6 X 3 = 18 u2
La superficie del rectángulo será, pues, la longitud de la base multiplicada por la altura:
S = b X a
Las unidades cuadradas pueden ser cualesquiera. Por ejemplo. sí empleamos el centímetro como unidad de longitud. tanto para medir la base como la altura. Tendremos entonces:
S = 6 cm • 3 cm = 18 cm2
3.3. Área del cuadrado.
El cuadrado, a diferencia del rectángulo, tiene la base de la misma longitud que la altura; por consiguiente. Si el lado mide a, la superficie será:
S = b • a = a • a = a2
Por ejemplo, la superficie de un cuadrado de 5 km de lado es:
S = (5 km)2 = 25 km2
3.4. Área del circulo.
Si vamos dibujando polígonos inscritos en una circunferencia, y vamos aumentando el número de lados, observamos lo siguiente:
a) El perímetro del polígono (P) se va aproximando a la longitud de la circunferencia (L);
b) La superficie del polígono (5) se va aproximando al área del círculo;
c) La apotema del polígono (ap) se va aproximando al radio de la circunferencia (r). Por consiguiente:
S = P x ap I 2 = L x r I 2 = 2 x π x r x r I 2
S = π X r2.
3.4. Área del triángulo
El área de un triángulo de lados a, b, c. y alturas correspondientes ha, hb y he es:
A = (1/2) a · ha= (1/2) b · hb = (1/2)c · hc
Si se conocen las longitudes de los tres lados, a, b, e, el área se puede calcular mediante la siguiente fórmula, llamada fórmula de Herón:
en donde p = (a+ b + c) /2 es el semiperímetro del triángulo.
4. GEOMETRÍA DEL ESPACIO.
Geometría del espacio, rama de la geometría que se ocupa de las propiedades y medidas de figuras geométricas en el espacio tridimensional. Entre estas figuras, también llamadas sólidos. se encuentran el cono, el cubo, el cilindro, la pirámide, la esfera y el prisma. La geometría del espacio amplía y refuerza las proposiciones de la geometría plana, y es la base fundamental de la trigonometría esférica, la geometría analítica del espacio. la geometría descriptiva y otras ramas de las matemáticas. Se usa ampliamente en matemáticas, en ingeniería y en ciencias naturales.
4.1. El cono.
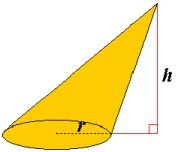
Cono (geometría), o cono circular recto, es el cuerpo de revolución engendrado por un triángulo rectángulo al girar alrededor de uno de sus catetos.
La hipotenusa del triángulo es la generatriz, g, del cono. El cateto sobre el cual se gira es la altura. h. El otro cateto es el radio. r. de la base.
El desarrollo de la superficie de un cono en el plano da lugar a un sector circular de radio g y ángulo (r/g) · 360º :
La superficie lateral de un cono recto es prg.
Por tanto. su superficie total es:
Alat = prg + pr2
El volumen de un cono recto es:
V = 1/3 π r2 h
4.1.1. Tronco de cono.
Un tronco de cono recto de bases paralelas es la porción de cono comprendido entre la base y una sección paralela a ella. Es el cuerpo de revolución generado por un trapecio rectángulo al girar alrededor del lado perpendicular a las bases.
Queda caracterizado por los radios de las bases, r y r', la altura. h. y la generatriz. g, entre las cuales se da la siguiente relación:
g2 = (r - r')2 + h2
El área lateral de un tronco de cono es:
Alat = p'(r + r')-g
Su volumen es:
V = p'(r2 + r'2 + rr') ·h/3
4.1.2. Cono oblicuo.
Un cono oblicuo es el cuerpo geométrico resultante de cortar un cono recto mediante un plano oblicuo a su eje y que corte a todas sus generatrices.
4.2. El cubo
El cubo es un poliedro regular formado por seis caras cuadradas.
El cubo es un ortoedro (sus caras son perpendiculares) con todas las aristas iguales.
El área total de un cubo de arista a es A= 6 X a2, su volumen es V = a3 y la longitud de su diagonal.
El cubo se llama también hexaedro regular o, simplemente. hexaedro.
4.3. El cilindro.
El cilindro o cilindro circular recto, es el cuerpo de revolución engendrado por un rectángulo al girar alrededor de uno de sus lados. El cilindro consta de dos bases circulares y una superficie lateral que, al desarrollarse, da lugar a un rectángulo. La distancia entre las bases es la altura del cilindro. Las rectas contenidas en la superficie lateral, perpendiculares a las bases, se llaman generatrices.
Un cilindro recto queda determinado mediante el radio de la base, r, y la altura, h. Su área total es:
Atotal = Alateral + 2Abase = 2prh + 2pr2
Su volumen es:
V = Abase · altura = pr2h
4.3.1. Cilindro oblicuo.
Un cilindro oblicuo es el que resulta de cortar un cilindro recto por dos planos paralelos que cortan oblicuamente a todas las generatrices.
Las bases de un cilindro oblicuo son elipses. Su altura es la distancia entre los planos que contienen las bases. Su volumen es:
V =Abase · altura
4.4. La pirámide.
Pirámide, poliedro limitado por una base. que es un polígono cualquiera, y varias caras laterales. que son triángulos con un vértice común llamado vértice de la pirámide.
La altura de la pirámide es la distancia del vértice a la base. Una pirámide se llama triangular. cuadrangular. pentagonal... según que su base sea un triángulo, un cuadrilátero, un pentágono...
Una pirámide es regular si su base es un polígono regular y el vértice se proyecta (cae perpendicularmente) sobre el centro de la base. En una pirámide regular las caras laterales son triángulos isósceles cuyas alturas se llaman apotemas de la pirámide.
El área lateral de una pirámide regular (suma de las áreas de las caras laterales) es:
y el área total:
Atot = Alat +Abase
El volumen de una pirámide es la tercera parte del producto del área de la base por la altura:
4.4.1. Tronco de la pirámide.
Un tronco de pirámide es el poliedro comprendido entre la base de la pirámide y un plano que corta a todas las aristas laterales.
Si el plano es paralelo al plano de la base se dice que el tronco es de bases paralelas. La distancia entre las bases es la altura del tronco. Un tronco de bases paralelas de una pirámide regular está formado por dos bases. Polígonos regulares semejantes. y varias caras laterales que son trapecios isósceles. Las alturas de estos trapecios se llaman apotemas de estos troncos.
El área lateral de un tronco de pirámide de bases paralelas es:
Alat = semisuma de los perímetros de las bases · apotema
El volumen de un tronco de pirámide. Cuyas bases son paralelas y tienen superficies B y B'. y cuya altura es h. se obtiene mediante la fórmula siguiente:
4.5. La esfera
La esfera es el cuerpo de revolución que se obtiene al girar un semicírculo alrededor de su diámetro. El centro y el radio de la esfera son los del semicírculo que la genera.
La superficie de la esfera o superficie esférica puede definirse también como el lugar geométrico de los puntos del espacio cuya distancia al centro es igual al radio.
Un plano y una esfera pueden ser exteriores (sin puntos comunes), tangentes (con un solo punto común) o secantes. si el plano atraviesa la esfera.
La intersección de una esfera con un plano es un círculo cuyo radio, r. se obtiene conociendo el radio de la esfera. R. y la distancia. d, del plano al centro de la esfera:
r2 = R2 -d2
Si el plano pasa por el centro de la esfera (la corta diametralmente), el círculo que determina en ella se llama círculo máximo y la circunferencia correspondiente circunferencia máxima.
El área de la superficie esférica es:
A=4pR2
El volumen de una esfera es:
V= 4pR3/3
4.6. El prisma.
El prisma es un poliedro limitado por dos polígonos iguales, llamados bases, situados en planos paralelos, y por varios paralelogramos, llamados caras laterales.
